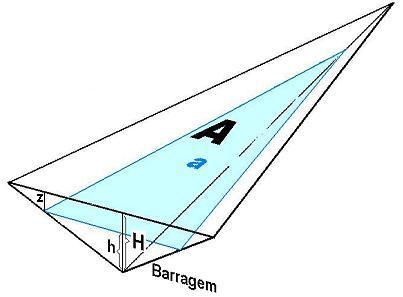
A method for determining areas as a function of depth
When it is desirable to calculate what area of a hydroelectric reservoir occupies the strip whose depth ranges from zero to a given depth, for example the strip with depth ranging from zero to 20m, you can use the method here presented called the inverted pyramid. This method uses as a reservoir model the “inverted pyramid” of the figure, and it is necessary to know the size of surface area A and dam depth H. Although the model is very simple, there has been reasonable agreement with known areas, determined by topography.
Figure. Inverted pyramid. Model to determine areas
Assuming the water surface area to be A when the dam depth is H is is possible to calculate the area a that the water surface (colored in the figure) would have for depth h. It is easy to show that area a is proportional to the square of depth h, in other words
a = c x h2,
where c is the proportionality constant. This constant is:
c = A/H2
In the following lines, by specifying z as the depth limit until where there is bubble emission, the area a will be identified as the area that does not emit bubbles.
After it is possible to calculate, by difference, the area S that emits bubbles, bounded by the shore and depth z. From bubble emission measurements maximum depth z is determined until where bubble emissions occur and h is calculated being h=H–z. The area S which emits bubbles with then be S=A–a, or
S = A – (A/H2)xh2.
Application of this method to two reservoirs:
1 – Tres Marias reservoir (on the São Francisco river, A=1009,32(km)2, H=50,2m). Assuming there is bubble emission from the shore to a depth of z= 23,3m, h= 26,9m is found and the bubble emitting area S=719,50(km)2 is calculated, to be compared with the known area, calculated from map contour lines, of 693,57(km)2. An overestimatimation of 3,7% is noted.
2- Tucuruí reservoir(on the Tocantins river, A=2430(km)2, H=65,5m). Assuming there is bubble emission from the shore to a depth of z=20,4m, h= 45,1m is found and the bubble emitting area S=1278(km)2, to be compared with the known area, calculated from map contour lines, of 1502,35(km)2. An underestimatimation of 15% is noted.